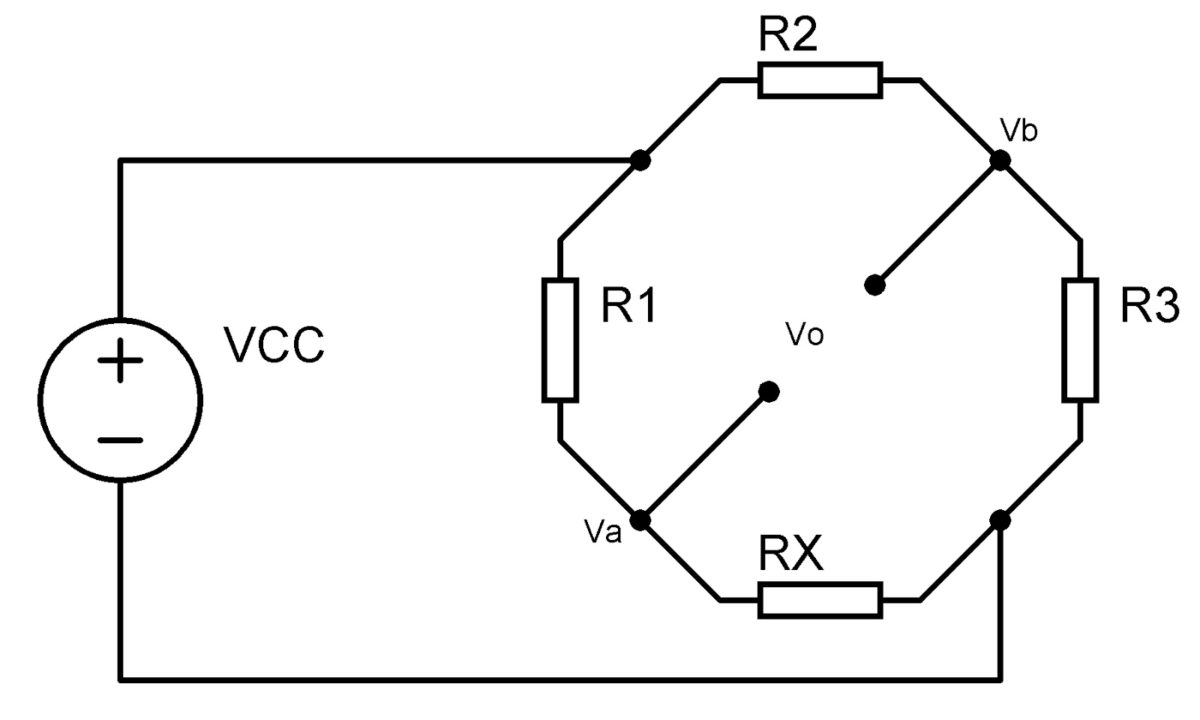
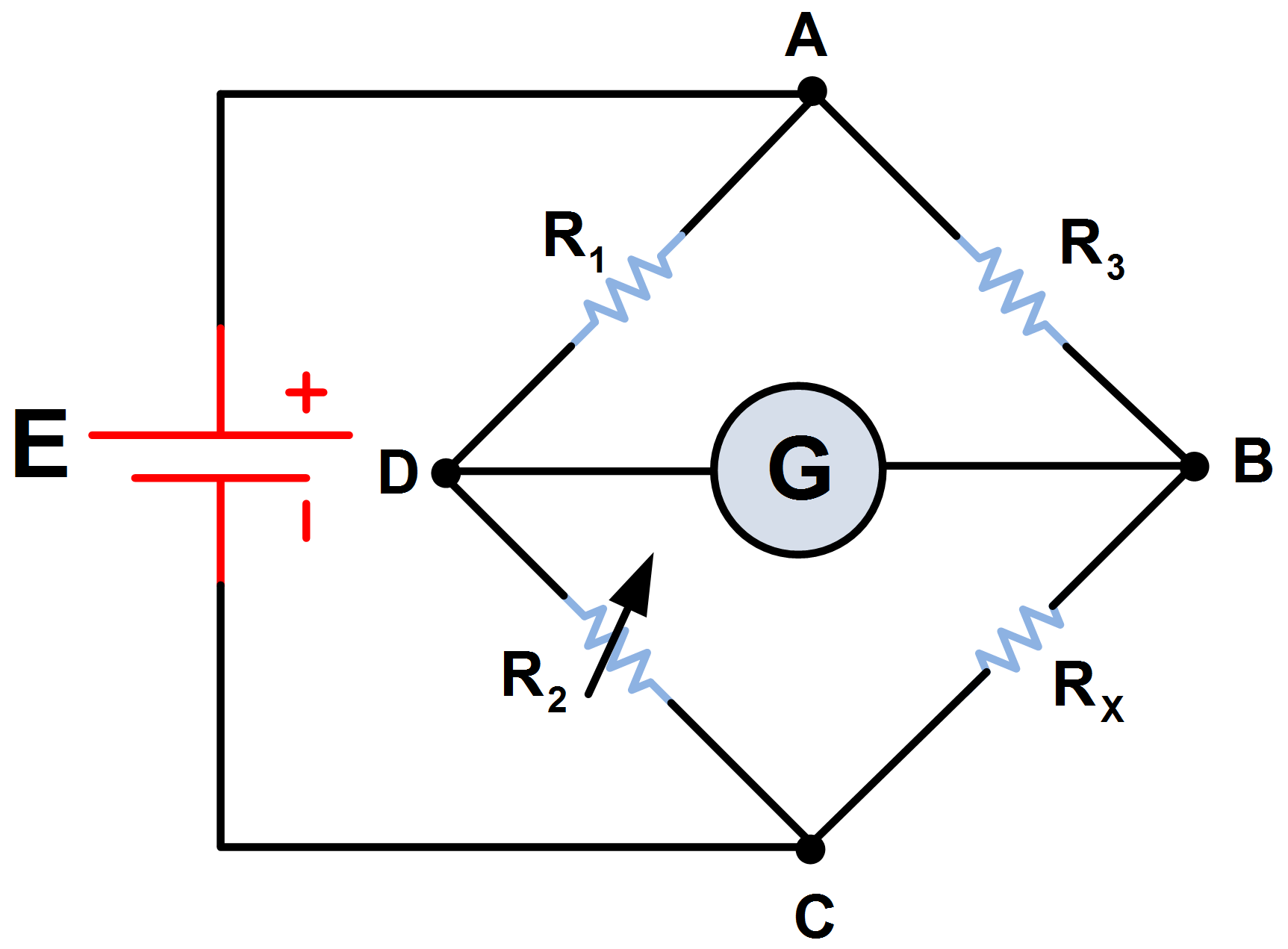
El puente de Wheatstone es un circuito eléctrico que cumple con la función de medir la oposición del paso de corriente de un dispositivo, esto también se conoce como resistencia. En el presente artículo ahondaremos a detalle acerca de este instrumento de medición.
Índice del Artículo
¿Qué es el Puente de Wheatstone?
El puente de Wheatstone es un método que funciona por medio de un circuito eléctrico, cuyo objetivo es medir de manera exacta la resistencia desconocida de un dispositivo. El mismo está conformado por cuatro resistencias creando de esta forma un circuito cerrado, por lo que una de ellas es la que se pretende medir.
Historia
Este circuito eléctrico fue desarrollado en el año 1833 por el experto en electricidad Samuel Hunter Christie. No obstante, fue hasta el año 1843 que el científico Charles Wheatstone pudo identificar sus usos, por lo que se considera dentro de la historia que él fue el fundador de este instrumento de medición. Al descubrir todos sus usos como método para calcular la resistencia desconocida, se considera una de las técnicas más precisas para este fin.
Acerca del inventor
Charles Wheatstone nació en el Reino Unido el 6 de febrero de 1802. El mismo creció en una familia que se dedicaba al ámbito musical, su padre hacía y vendía sus canciones, mientras que su tío tenía una tienda musical en donde el joven trabajó en 1816. Estar rodeado de instrumentos influyó en su educación autodidacta y ya para el año 1823 había publicado su primera investigación.
En 1829 fue nombrado como Físico experimental en la King’s College de Londres en 1834. Luego de esto, el físico tuvo un mayor interés en la investigación de la acústica, la óptica y la electricidad. Durante sus estudios en el campo de la óptica, Wheatstone diseña un estereoscopio en donde se combinan dos imágenes vistas desde ángulos diferentes, esto con el fin de crear una imagen tridimensional.
Ya para el año 1840, por primera vez en la historia, realiza la medición de la manera en que se propaga la corriente eléctrica en los conductores metálicos. En 1843 crea las resistencias variables las cuales están dirigidas al uso de un instrumento diseñado con el fin de medirlas, para esto, las comparaba en un circuito eléctrico diseñado a partir de la ley de Ohm. Dicho circuito recibe el nombre del puente de Wheatstone, debido a que fue él quien lo dio a conocer, a pesar de que se creador fue Samuel Hunter Christie.
Características
El Puente de Wheatstone está formado por cuatro terminales eléctricos, de los cuales dos le transmiten alimentación eléctrica a todo el dispositivo y los dos restantes se encargan de recibir la señal que se propaga durante la salida y que va directo al circuito que sirve como acondicionador.
Las resistencias por sí solas no poseen un voltaje fijo de su medida en Ohmios. En realidad, al inicio poseen un valor conocido como Ro y luego se le agrega otro el cual estará atado a las magnitudes de las mismas. Al no tener un valor determinado, es necesario recurrir a un dispositivo que no presente problemas en la medición, con esto hacemos referencia al Puente de Wheatstone, que consigue que el error en la medida sea lo menor posible.
De esta manera, el dispositivo al estar constituido por cuatro resistencias, de las cuales una es desconocida y no posee un valor fijo de Ohmios, se entiende de la siguiente forma:
Rx = R0 (1 + X)
- Rx = valor total de la resistencia.
- R0 = el valor inicial de la resistencia; X = es el valor correcto que se desconoce.
Este dispositivo está diseñado para emplear tres resistencias y un sensor en una determinada posición en el circuito. A los dos terminales que generan energía se les denomina como Vcc y masa, la energía que generan la hacer circular por todo el sistema del instrumento. Mientras que los otros terminales de salida se conocen como A y B, cuya función es poder recolectar las variaciones de tensión. Matemáticamente se lee de la siguiente manera:
VA = (VCC / (R2 + Rx)) X R2
VB = (VCC / (R1 + R4)) X R4
VAB = VA – VB [(VCC / ((R2 + RX)) X R – [(VCC / (R1 + R4)) X R4
Al resolverlo de forma matemática, se termina obteniendo una ecuación que se entiende de la siguiente forma:
Vs = ((Vcc x K) / (K + 1)2)• X
- Vs = es el valor de la tensión durante la salida; K = R2 / R0 = R1 / R4
- X= Es el valor de la variación inicial conocida como R0 respecto de la magnitud a medir.
Como elemento esencial se utiliza una galga extensiométrica, la misma es un sensor que mide tensión, carga, posición y más, pero su uso fundamental para este instrumento, es como detector de la magnitud de las resistencias con respecto a la magnitud de la presión.
Para realizar esto, se debe emplear una fuerza que vaya en sentido longitudinal sobre dicha galga, al hacer esto, la misma se recoge y vuelve a estirarse, esta deformación es lo que hace posible las variaciones en la tensión de las resistencias.
Para comprender el comportamiento de cada una de las galgas involucradas en este tipo de instrumento es necesaria una ecuación, esta se expresa de la siguiente manera:
Rg = R0 x ( 1 + (K1x E)
- Rg = Se entiende como la resistencia propia de la galga.
- R0 = Representa la resistencia de inicio de la galga sin haberse deformado.
- K1 = Es una constante que dependerá del material de soporte con el que se trabaje.
- E =Se entiende como la deformación lineal que se da en la galga.
En resumen, el valor propio de la variación de la galga es causado por una constante K1 por medio de un factor E, el cual dependerá del nivel de deformación del material soporte. Para poder acondicionar la señal de una galga extensiométrica, se debe integrar la misma dentro del Puente de Wheatstone y así obtener la deformación requerida, expresada en voltios, entre los terminales A y B.
Sensibilidad del instrumento
Esta parte es fundamental para el Puente de Wheatstone, puesto que hace referencia a la sensibilidad de la respuesta, lo que contribuirá a tener resultados más precisos y exactos. Dicha sensibilidad viene dada por el número de divisiones que desencadene el galvanómetro cuando se produce alguna variación en el equilibrio de la resistencia 2 a causa de la resistencia desconocida.
¿Para qué sirve el Puente de Wheatstone?
Como ya se había comentado, este instrumento se emplea para poder medir la oposición que tiene la corriente eléctrica de un dispositivo cuando se transmite, también conocida como la resistencia. Al estar conformado por cuatro resistencias, a tres de ellas ya se les conoce su valor en el voltaje, mientras que la cuarta es la desconocida por lo que su fin es calcular el valor preciso de esta.
Es válido destacar que por medio de este instrumento también se puede realizar otra función, no solo permite conocer el valor en voltaje de una resistencia, sino que también proporciona su valor total al compararla con otra resistencia y además, determina las variaciones que tienen lugar en las mismas cuando se les manipula.
¿Cómo funciona?
Para entender el funcionamiento del Puente de Wheatstone es vital comprender su configuración, puesto que a partir de esta es que se realizarán los cálculos. En primera instancia, hay un terminal que conduce el polo positivo de electricidad, en este se encuentran conectadas las resistencias 1 y 3. Mientras que las resistencias 2 y 4 están conectadas a tierra, entiéndase por tierra a cualquier objeto de metal. La resistencia 4 es la desconocida, por lo cual es la que se procederá a medir, por su parte, la resistencia 2 será considerada como la variante y el punto de equilibrio.
Se ha de notar que las resistencias 1 y 2 son divisores de tensión, de igual manera lo son la 3 y 4. Se tiene la hipótesis de que todos los voltajes para las resistencias son iguales, esto significa que la división entre las tensiones de estas debería dar un total de cero. Si se desconoce alguno de los valores de voltajes para las tres primeras resistencias, esto se puede averiguar fácilmente por el código de colores que presentan.
Ahora con respecto a su funcionamiento, se puede iniciar por armar un circuito para la resistencia desconocida. Una vez hecho esto, se procede a hacer la polarización, esto puede ser con un voltaje cualquiera pero es recomendable que este voltaje ronde hasta el valor 5, no se debería exceder de este. No obstante, al mismo se le puede hacer un ajuste por medio de un amplificador operacional.
Al ser la resistencia 2 de carácter manipulable, esta es apropiada para poder medir el voltaje de salida, para esto lo que se busca es que se iguale a cero. Haciendo que la resistencia que se desea conocer sea un evento nulo. Ya teniendo ajustado todo el sistema, los cambios en el voltaje de la resistencia desconocida empezarán a hacer que el sistema se salga de la zona de equilibrio impuesta por la resistencia 2 y esta medición será dada por el voltaje de salida.
Con respecto a los cálculos para la medición de la resistencia desconocida, lo primero es conocer la igualdad de la resistencia en donde ocurre lo siguiente:
R2/R1=Rx/R3
Esta es la manera gráfica en la que se entiende que las primeras dos resistencias dan con la división de la tensión del circuito y por ende este resultado es el mismo si se hiciera con la resistencia desconocida dividida entre la tercera resistencia.
Para poder dar con los resultados acerca de la variación de voltaje de la resistencia desconocida por medio del voltaje de salida, se debe proceder a realizar un análisis del circuito construido. Si se tiene en cuenta que este instrumento posee una resistencia lo suficientemente alta, para poder dar con el voltaje diferencial de las dos primeras resistencias, la fórmula a aplicar es la siguiente:
Vg=(R2/R1+R2 – Rx/Rx+R3) – Vs
Variantes
Las variantes resultantes de este instrumento pueden ser empleadas para el cálculo de las impedancias que extienden el concepto de las resistencias pero aplicándose en circuitos internos. De un mismo modo, se aplica para medir la capacitancia que hace referencia a la carga eléctrica que tienen los instrumentos, y por último se emplea para las inductancias que sería la oposición de electricidad puesta en una bobina en la que se almacene la energía del circuito.
La disposición de este instrumento también es muy solicitada en el campo de la electrónica. No obstante, para poder llevarlo a cabo en este ámbito se debe sustituir al menos una de las resistencias de los sensores, dado que al hacer esto se genera una salida proporcional a la variación utilizada. En este instrumento viene integrado lo que se conoce como galvanómetro, el mismo sirve para medir la tensión y conocer en qué dirección es dada la carga eléctrica, justo al lado de este es colocado el amplificador.
A pesar de que el Puente de Wheatstone es el más reconocido y empleado para determinar el voltaje de las resistencias, existen otros medios que pueden cumplir fácilmente con esta función cuando el mismo no es adecuado para las tareas. Dichos medios o métodos pueden ser los siguientes:
- Puente de Carey Foster: El mismo también es un circuito eléctrico pero empleado únicamente para poder realizar mediciones de resistencias de pequeños voltajes.
- Puente de Kelvin: Este circuito al igual que el anterior, sirve para calcular resistencias de pequeño voltaje pero en un sistema conformado por cuatro terminales eléctricos.
- Puente de Maxwell: Este circuito es una versión actualizada del puente de Wheatstone. Las modificaciones realizadas a esta versión permiten que se logren medir con precisión las inductancias y capacitancias.
- Puente de Hay: Garantiza medir únicamente las inductancias del circuito eléctrico.
- Puente de Wien: Este es un modelo diferente, puesto que es considerado un oscilador eléctrico, el mismo lo que hace es producir una señal eléctrica que va variando en sistema un continuo, por lo general es una onda eléctrica conocida como senoidal.
Usos del instrumento
El uso de este instrumento es exclusivo del ámbito electrónico. No obstante, se le ha encontrado una aplicación práctica dentro de esta área más allá de solo medir las resistencias desconocidas en un sentido experimental.
Este instrumento se encuentra integrado dentro de muchos dispositivos electrónicos, como por ejemplo los medidores de la presión conocidos como manómetros y en dispositivos tecnológicos de vacío como los resonadores. También se ha encontrado que sirve como un detector de fenómenos como la resonancia paramagnética, que es una técnica para detectar electrones libres.
Factores que inciden en su precisión
Para que exista exactitud y precisión en los cálculos realizados por este instrumento, es necesario cumplir con varios factores, puesto que de lo contrario, los resultados encontrados para el voltaje de la resistencia estarían erróneos. Dichos factores son los siguientes:
- Que exista precisión y exactitud en las tres primeras resistencias: Para que esto ocurra los valores en los voltajes de estas deben ser iguales a cero, por ende, la expresión de la resistencia desconocida no puede resultar de la siguiente manera: Rx= R1 x R2/R3
- Si ocurre de esta forma significaría que existe un error relativo de la resistencia desconocida, que vino dado por los errores relativos de las tres primeras resistencias.
- Precisión en los valores de voltaje de las resistencias 1 y 3: Para lograr esto, los valores de voltaje de estas resistencias deben ser lo más bajos posibles, ya que cuando esto ocurre se crea una corriente eléctrica mayor en el circuito, lo que facilita la detección de las variaciones en la resistencia desconocida.
- El valor de la fuente: Si los valores de esta fuente son altos, entonces la corriente eléctrica que recorre el circuito se incrementaría y el resultado sería un proceso más sencillo para determinar las variaciones de la resistencia a conocer. No obstante, se recomienda para este factor realizar ciertos ajustes tomando en cuenta las limitaciones que se podrían presentar por la potencia de las baterías integradas.
- La sensibilidad del galvanómetro: Con respecto a este factor, se debería esperar que la sensibilidad de este dispositivo integrado sea lo más alta posible para que se pueda apreciar mejor la corriente de energía, si esto es así, los ajustes que se realicen con respecto a las resistencias se harán con mayor precisión llevando dicha corriente a cero, que es lo deseado.
La Ley de Ohm
En vista de que el puente de Wheatstone es un instrumento empleado en el ámbito de la investigación de la física, es lógico pensar que su funcionamiento está regido por una ley, en este caso es la ley de Ohm, puesto que es esta la unidad de medida por la cual se conoce el voltaje de las resistencias involucradas en su circuito eléctrico.
Esta ley fue postulada por el físico y matemático Georg Simon Ohm, que en el siglo XIX dio con el descubrimiento de que la corriente de electricidad que se conduce por un metal, es proporcional al potencial eléctrico del mismo. Al descubrir esto tuvo la idea de crear las resistencias eléctricas. Dicha ley se puede expresar en la siguiente fórmula:
V= R x I
- V= Es la diferencia en el potencial eléctrico, entendiéndose como el nivel de carga que posee cada unidad para hacer conducir la energía eléctrica. Esta diferencia es medida en voltios.
- I= Hace referencia a la intensidad de la corriente eléctrica, la cual es medida como amperios.
- R= Alude a la resistencia eléctrica que es tomada como Ohmios.
Es importante conocer un poco más sobre esta última, por ser el punto de estudio de este instrumento. La resistencia según Ohm se entiende como la dificultad u oposición con que las cargas de energía eléctrica se desplazan por medio de un conductor.
Una mejor forma de reflejar este concepto un poco abstracto es comparándola con el agua, la misma puede verse como la fricción que se produce cuando el agua pasa por un tubo. Si este ofrece una superficie pulida y lisa, la resistencia del paso del agua es casi nula, por otro lado, si el mismo está lleno de deformaciones y desperdicios, el paso del agua a través de él sera mucho más lento.
La resistencia eléctrica guarda relación con la interacción que realizan los electrones encargados de la conductividad de la energía, esto sucede a medida que se mueven de átomo a átomo por el conductor.
Para poder conocer el valor de la resistencia que tiene un material con respecto a su paso de corriente, se debe tener conocimiento primero de la resistividad o la resistencia específica del mismo material, este elemento se conoce comúnmente como P (rho). De esta manera, se procede a utilizar la siguiente fórmula:
R= P x I/S
- P= Sería entonces el coeficiente de la resistencia específica del material que se da en una temperatura precisa.
- I= Hace referencia a la longitud del material, esta es medida en metros.
- S= Se entiende como la superficie en la que se encuentra dispuesto el material.
Campo experimental del Puente de Wheatstone
El uso experimental de este instrumento se ve de manera frecuente en los laboratorios de física, en ellos se presenta este circuito eléctrico ya terminado y se solicita realizar los cálculos de algunas resistencias involucradas. En estos casos, se utiliza como conductor entre las resistencias un hilo de alambre puesto en el reóstato, que es lo que ocasiona la resistencia variable.
El dispositivo del galvanómetro se encuentra inactivo para el momento por cuestiones de seguridad, por lo que se debe encender a la hora de proceder a utilizar el sistema del instrumento. No obstante, antes de esto es importante que la medida que limita el paso de la corriente se encuentre en 25 mA, de una misma manera, el voltaje de la salida de las resistencias debe estar también a este valor.
La resistencia a conocer puede ser cualquiera, puesto que estos diseños de laboratorio vienen con valores variables para cada una. Se escogen las dos resistencias que serán las que transmitan el paso de energía hacia el circuito y las restantes serán las conductoras de la salida.
Ha sido todo por el artículo de hoy, esperamos que la información proporcionada le haya sido de gran utilidad. Le hacemos la invitación a leer también: Flexómetro y Voltímetro